신장 트리(Spanning Tree)란, 연결 그래프의 부분 그래프이며 모든 정점과 간선의 부분 집합으로 구성되는 트리입니다. 이 때, 모든 정점에는 하나 이상의 간선에 연결되어 있어야 합니다.
최소 신장 트리(Minimum Spanning Tree. MST)는 만들 수 있는 신장 트리 중에서 간선 비용의 합이 최소인 신장 트리를 말합니다. MST의 간선 개수는 정점의 수 - 1개입니다. 간선들의 비용 합이 최소인 경우는 여러 개 나올 수 있으므로 하나 이상 존재합니다.
이런 MST를 만드는 대표적인 방법으로는 프림 알고리즘과 크루스칼 알고리즘이 있습니다. 프림 알고리즘은 정점을 성택하여 확장하는 방법이고, 크루스칼 알고리즘은 간선을 선택하여 확장하는 방법입니다. 이번 포스팅에서는 프림(Prim) 알고리즘을 알아보도록 하겠습니다.
크루스칼 알고리즘 : https://withhamit.tistory.com/322
프림 알고리즘은 정점 하나를 시작지점으로 두고 해당 정점에 연결된 간선 중 최소인 간선부터 확인하며 해당 간선으로 연결된 정점이 현재 만들고 있는 신장트리에 속하지 않았다면 채택합니다. 그리고 새로 채택한 정점에 연결되어 있는 간선들도 포함하여 아까와 같은 방법을 반복하면서 이를 모든 정점이 선택될 때 까지 즉, 정점-1개의 간선을 선택할 때까지 반복합니다.
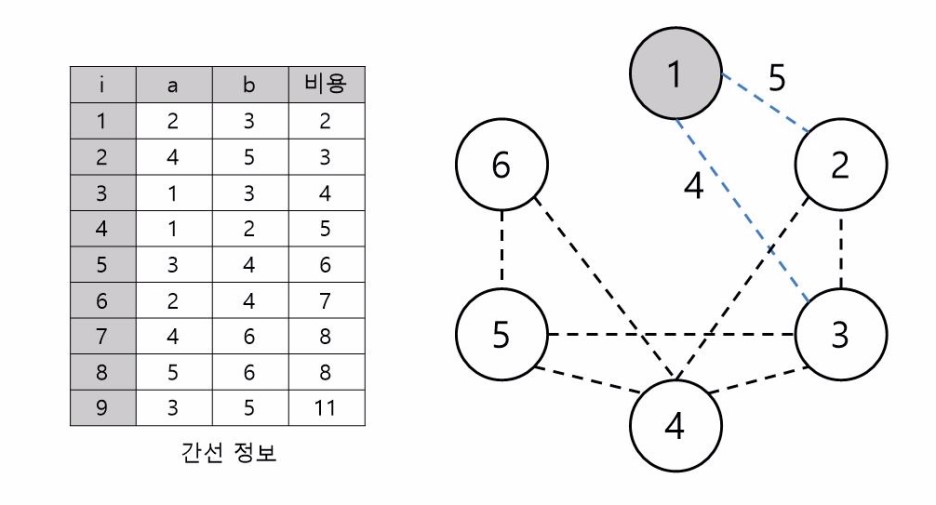
이제 [그림 1]과 같은 그래프의 MST를 프림 알고리즘을 이용하여 만들어 보겠습니다.
우선 정점 1부터 선택합니다. MST를 완성했을 때 모든 정점은 연결되어 있으므로 아무 정점에서나 시작해도 같은 가중치를 가지는 MST를 만들 수 있습니다.
1번 정점을 선택했을 때 간선들 중 최소 값은 정점 3과 연결된 4입니다. 이 때 정점 3은 아직 선택되지 않았으므로 해당 간선을 이용하여 정점 3을 연결해줍니다.

이제 정점 3과 연결된 간선들도 포함하여 최소 가중치 2를 가지는 간선을 보면 정점 2와 연결되어 있습니다. 이 때 정점 2는 아직 선택되지 않았으므로 해당 간선을 채택합니다.
이제 정점 2와 연결된 간선들도 포함해서 최소 가중치를 가지는 간선을 찾아봅니다.
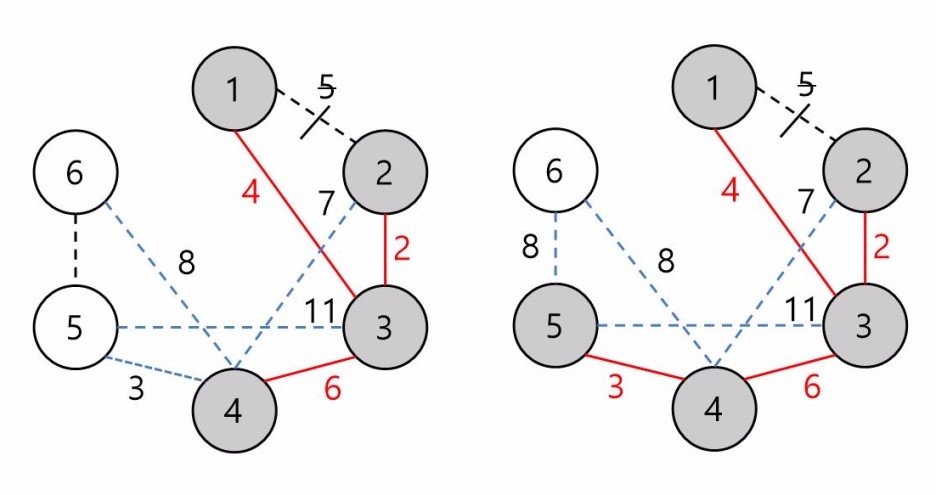
최소 가중치는 5인데 이 간선은 이미 선택된 정점인 1과 연결되어 있습니다. 따라서 해당 간선은 무시하고 그 다음 작은 가중치를 가지는 간선을 찾습니다. 그래서 가중치 6인 간선을 찾을 수 있고 이는 아직 선택되지 않은 정점 4와 연결되어 있으므로 MST에 포함할 수 있는 간선입니다.
정점 4와 연결된 간선들도 포함하여 아직 선택되지 않은 정점과 연결된 최소값의 간선을 찾아보면 [그림3]의 오른쪽 그림과 같아집니다.(정점 5와 연결된 가중치 3인 간선 선택)
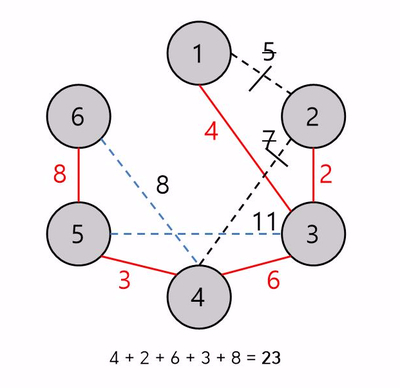
마지막으로 간선의 가중치가 최소인 8을 연결하면 모든 정점이 선택되고 정점-1개의 간선이 채택되었으므로 MST를 완성했다고 볼 수 있습니다.
채택한 간선들의 합은 23이 되고 이가 곧 MST를 만드는 비용이 됩니다.

처음에 "간선들의 비용 합이 최소인 경우는 여러 개 나올 수 있으므로 하나 이상 존재한다"는 이야기를 했었는데 [그림 4]의 마지막 단계에서 보면 간선 가중치가 8인것은 2개가 있고 간선 2개다 아직 선택하지 않은 정점인 6과 연결되어 있어서 채택할 수 있습니다. 따라서 두 간선을 각 각 선택했을 때 나오는 그림은 [그림 5]와 같고 두 트리 모두 MST 조건을 만족한다는 것을 알 수 있습니다. 이와 같이 MST는 가중치의 값은 같을 수 있어도 모양은 여러 개 나올 수 있습니다.
프림 알고리즘을 구현 시 탐색한 정점과 연결되어 있는 간선들의 정보를 우선순위 큐에 저장해서 최소 가중치를 가지는 간선을 O(lgE)만에 찾을 수 있습니다.
MST를 이용하는 문제입니다.
네트워크 연결(1922) : https://www.acmicpc.net/problem/1922
소스코드 : https://github.com/fpdjsns/Algorithm/blob/master/tip/%ED%94%84%EB%A6%BC.cpp
'알고리즘 이론' 카테고리의 다른 글
| KMP 알고리즘 (0) | 2020.02.09 |
|---|---|
| 크루스칼 알고리즘(Kruskal’s algorithm) (0) | 2020.02.06 |
| 세그먼트 트리(Segment Tree) (0) | 2020.02.02 |
| 트리 순회(전위 순회, 중위 순회, 후위 순회) (2) | 2019.10.04 |
| 벨만포드 알고리즘 (Bellman-Ford algorithm) (0) | 2019.09.26 |




댓글