만든 사람이 Knuth, Morris, Pratt 여서 Knuth–Morris–Pratt(KMP) 알고리즘이라 합니다.
문자열 알고리즘 중 하나로 문자열 에서 다른 문자열을 검색하는 알고리즘입니다.
단순하게 문자열(S) "ABCABDABCABC" 에서 문자열(P) "ABCABC"를 검색해봅시다.

S, P 모두 가장 앞에서부터 같은지 비교합니다.
(1) ~ (5) 는 문자가 같기 때문에 다음 문자를 비교합니다.
(6) D, C는 다르기 때문에 문자열 P를 찾을 수 없습니다.

이제 S 문자열의 인덱스 1부터 다시 비교합니다.
(1) B, A는 다르기 때문에 문자열 P를 찾을 수 없습니다.

문자열 P를 찾을 때까지 이를 반복합니다.
문자열 S 인덱스 6부터 시작하는 부분문자열에서 문자열 P를 찾을 수 있었습니다.
시간복잡도는 문자열 P의 길이만큼을 문자열 S의 모든 인덱스를 시작 지점으로 비교해야 하므로 O(|S||P|) 입니다. |S|, |P|를 모두 N이라 한다면 O(N^2)가 됩니다.
이를 KMP 알고리즘을 적용하여 찾아봅시다.

이전 방법에서는 문자열이 같지 않다고 판단된다면 문자열 S의 부분문자열 시작인덱스를 1만 증가시켜서 문자열이 같은지 다시 비교했습니다.
KMP 알고리즘을 사용한다면 시작인덱스를 1이 아닌 3만큼 증가시켜 문자열이 같은지 다시 비교합니다.
어떻게 바로 3을 증가시킬 수 있는 걸까요?
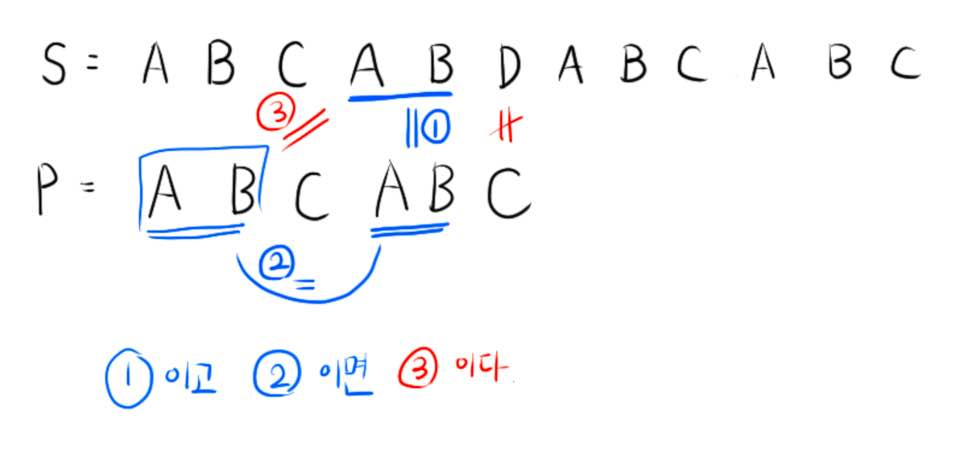
[그림 5]를 보면 P의 부분문자열들 P[0~1]과 P[3~4]은 같은 것을 확인할 수 있습니다.
즉, P의 문자열들 중 틀린 문자가 나오기 이전까지 탐색한 부분문자열 P[0~4]을 보았을 때,
접두사(prefix) 접미사(suffix)의 최장 동일 문자열이 P[0~1], P[3~4]이고 이를 이용하여 다음 탐색 인덱스를 구할 수 있습니다. P[3~4]과 S[3~4]이 같다는 것을 탐색하면서 알수 있고 추가로 P[0~1], P[3~4]가 같다는 것을 알고 있다면 S[2~3], P[0~1]이 같다는 것이 증명됩니다.
삼단 논법입니다.
1 - 조건) P[3~4] == S[3~4]
2 - 조건) P[0~1] == P[3~4]
3 - 결론) S[3~4] == P[0~1]
따라서 S[1], P[0]부터 다시 탐색을 시작하지 않고 S[5], P[2]가 같은지부터 탐색을 시작할 수 있습니다.
조건 1은 탐색 도중 알 수 있게 되는 사실입니다.
우리는 추가로 조건 2를 알 수 있는 배열을 구하면 됩니다.
예시에서 조건 2에 해당하는 P의 부분문자열은 P[0~4], "ABCAB" 입니다.
같은 부분은 "ABCAB", AB 입니다. 앞에서 말했다시피 이는 부분문자열의 접미사, 접두사가 같은 것들 중 최장길이입니다. 이를 저장하는 배열 pi를 만들어야 합니다.

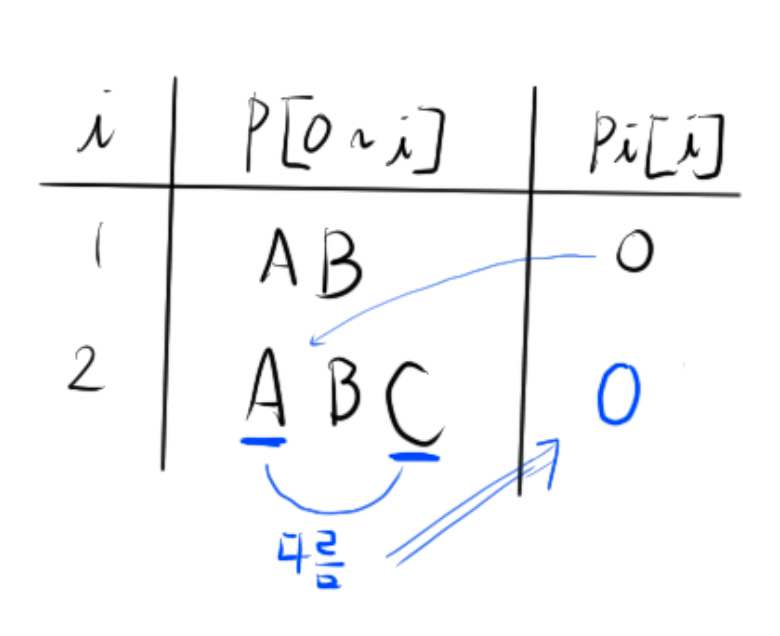
pi 배열을 구하면 위와 같습니다.

구한 pi 배열을 이용해서 어떻게 3칸을 이동하게 된건지 알아보겠습니다.
1. S[5]('D'), P[5]('C') 가 같지 않습니다.
2. 이전 배열들까지는 같았기 때문에 P[0~4]의 최장 공통 접미사, 접두사 길이를 가져옵니다. pi[4]는 [그림 6]을 보면 알 수 있습니다. 2입니다.
3. P[0~1] (인덱스는 0부터 시작하니까, 2개가 같음 = 0, 1) 부분문자열이 S[4~5]와 같다는 걸 알 수 있습니다. 따라서 P[3]과 S[5]가 같은지부터 다시 탐색하기 시작합니다.
예시에서는 P가 "ABCABC"이기 때문에 또 P[3], S[5]가 같지 않아 P[0]부터 다시 탐색해야 하지만,
만약 S="ABDABD...", P="ABDABC" 였으면 P[3], S[5]를 비교 시 같기 때문에 P[4~], S[6~]를 계속 탐색할 수 있어서 시간을 더욱 단축시킬 수 있습니다.
|S| = N, |P| = M 이라 했을 때, 문자열 S가 같은지 비교하는 인덱스가 감소하지 않고 증가하기만 하기 때문에 시간복잡도는 O(N+M) 입니다.

pi는 어떻게 만들 수 있는지 알아봅시다. P[i], P[pi[i-1]]가 같은 경우는 pi[i-1] + 1을 저장합니다.
P[i], P[pi[i-1]]가 다른 경우는 0을 넣으면 될 것 같지만 안되는 경우도 있습니다.

ABACABAB를 예로 들어봅시다. pi[7]을 구해봅시다.
1. P[3]('C'), P[7]('B')는 다릅니다.
2. P[7]에 바로 0을 넣어버리기에는 AB가 공통 접미사, 접두사라는게 우리 눈에 밟힙니다. 사실 pi를 채우는 로직도 [그림 7]에서 문자열 S에서 P를 찾는 방법과 비슷합니다. 문자열 P의 접미사, 접두사라 생각하지 않고 문자열 S(ABAB)에서 문자열 P(ABAC)를 찾는다고 생각해봅시다. S[3], P[3]이 같지 않기 때문에 pi[2] 인덱스로 다시 비교하는 겁니다. P[pi[2]] = P[1] = 'B'와 S[3]은 같습니다. 따라서 pi[2] + 1 = 2를 pi[7]에 저장해줍니다.
|P| = M이라 할 때, pi 배열을 구하는 시간복잡는 KMP 와 비슷한 원리로 O(M)입니다.
KMP 알고리즘이 가장 유용하게 적용되는 예시는 S = "aaaaaaaaaaaaaaaaaaaaab", P = "aaaaaab" 인 경우입니다.
즉, P의 가장 마지막 문자 이전까지의 부분문자열이 문자열 S에 연속으로 나오는 경우입니다. S의 가장 뒤에 문자열 P가 나오지만 |P|-1 만큼의 탐색을 거의 |S| 만큼 반복해야 합니다.
O(NM)으로 문자열 검색을 할 때의 worst case입니다.

참고로 제가 많이 사용하는 C++의 string.find의 시간복잡도도 O(NM)으로 구현되어 있습니다.
문자열 검색 문제가 나왔을 때, 제한 사항을 읽어보고 KMP를 적용해야 하는지에 대한 고려도 필요할 것 같습니다.
'알고리즘 이론' 카테고리의 다른 글
| 동전 교환(CC: Coin Change) (5) | 2020.02.23 |
|---|---|
| 다이나믹 프로그래밍(Dynamic Programming) (0) | 2020.02.22 |
| 크루스칼 알고리즘(Kruskal’s algorithm) (0) | 2020.02.06 |
| 프림 알고리즘(Prim's algorithm) (0) | 2020.02.06 |
| 세그먼트 트리(Segment Tree) (0) | 2020.02.02 |




댓글