세그먼트 트리는 구간의 값을 저장하는 트리입니다.
1~N인 수열이 있을 때, "인덱스가 a~b인 수들의 합을 구하고 싶다."
혹은, "a~b번째 수들 중 최소 값이나 최대값을 구하고 싶다." 같은 경우 사용합니다.
세그먼트 트리는 이진 트리 모습을 가지며 자식 노드는 부모 노드의 범위를 반 씩 가지고 있습니다. 즉, 부모 노드가 1~5까지의 구간합을 가지고 있다면 자식 노드의 왼쪽 자식은 1~3의 구간 합을 가지고 오른쪽 자식은 4~5까지의 구간 합으로 나눠가집니다.
수열의 크기(N)가 5인 수열 A = {1, 2, 3, 4, 5}의 구간 합을 구하고자 할 때 사용하는 세그먼트 트리를 생성해 봅시다. 인덱스(i)는 접근이 쉽게 0이 아닌 1부터 시작하였습니다.

처음 상태의 세그먼트 트리는 다음과 같습니다.
각 노드의 파란색 글씨가 구간을 뜻하고 검정색 글씨가 노드 값을 의미합니다. 현재는 트리에 수열의 아무 수도 넣지 않았기 때문에 모든 노드값은 0이 됩니다.
루트 노드에는 1~5(1~N) 구간의 값, 여기서는 합을 구하려고 하니까 1~5번째 값들의 합을 저장합니다.
현재 노드의 구간을s~e라고 봤을 때, 왼쪽 자식의 구간은s ~ (s+e)/2이고, 오른쪽 자식의 구간은 (s+e)/2+1 ~ e입니다. 즉, 단노드를 제외한 노드들은 구간을 반으로 쪼개서 구간 합을 가지고 있는 자식 노드 2개를 가집니다.
이 때, 단노드에는 수열이 가지는 실제 값이 저장됩니다.([그림 1]의 파란색 부분) 노드가 포함하는 구간의 인덱스 s~e에서 s와 e가 같은 경우(s==e), 해당 노드는 단노드라고 볼 수 있습니다.

이제 수열의 값을 처음부터 넣어봅시다. 현재 넣고자 하는 인덱스를 i라고 합시다.
i가 1인 수를 넣으려면 노드의 인덱스와 i를 비교하여 단노드까지 내려갑니다. 여기서는 노드의 인덱스 범위가 1~1인 노드를 찾으면 되겠죠?
노드를 찾았으면 해당 단노드의 값을 A[i]로 갱신시킵니다.

그리고 내려왔던 길을 다시 거슬러 올라가면서 노드들의 값을 갱신시킵니다.
갱신시키는 것은 간단하게 자식 노드들의 값을 합친 값으로 갱신하면 됩니다.
1~2노드는 1(1 노드) + 0(2 노드) =1로 갱신합니다. 그리고 부모 노드로 올라갑니다.
1~2의 부모 노드인 1~3노드는 1(1~2 노드) + 0(3 노드) = 1로 갱신합니다. 마찬가지로 부모 노드로 올라갑니다.
1~5노드는 1(1~3 노드) + 0(4~5 노드) = 1로 갱신합니다. 루트 노드이므로 더 이상 갱신할 노드가 없고 따라서 트리의 갱신이 끝났음을 알 수 있습니다.

마찬가지로 2를 넣습니다.
단노드의 범위가 2~2인 노드를 찾아서 값을 갱신합니다.

1~2 노드 = 1(1 노드) + 2(2 노드) = 3
1~3 노드 = 3(1~2 노드) + 0(3 노드) = 3
1~5 노드 = 3(1~3 노드) + 0(4~5 노드) = 3[루트 노드 -> 종료]

단노드의 범위가 3~3인 노드를 찾아서 값을 갱신합니다.

1~3 노드 = 3(1~2 노드) + 3(3 노드) = 6
1~5 노드 = 6(1~3 노드) + 0(4~5 노드) = 6[루트 노드 -> 종료]
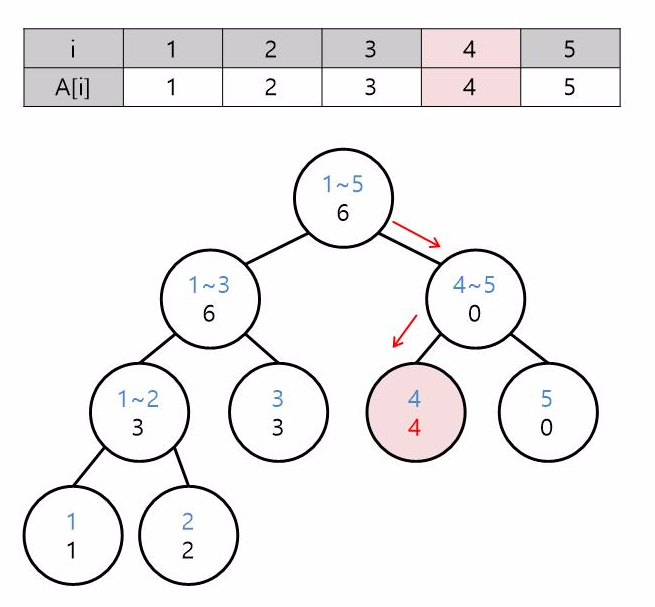
단노드의 범위가 4~4인 노드를 찾아서 값을 갱신합니다.

4~5 노드 = 4(4 노드) + 0(5 노드) = 4
1~5 노드 = 6(1~3 노드) + 4(4~5 노드) = 10[루트 노드 -> 종료]

단노드의 범위가 5~5인 노드를 찾아서 값을 갱신합니다.

4~5 노드 = 4(4 노드) + 5(5 노드) = 9
1~5 노드 = 6(1~3 노드) + 9(4~5 노드) = 15[루트 노드 -> 종료]
모든 수열의 값을 트리에 넣어서 A 수열의 구간 합을 구하기 위한 세그먼트 트리가 완성되었습니다.
완성된 트리에서 수열 A의 값이 변경되어서 트리를 갱신해야 할 때도 위의 방법과 마찬가지로 진행하면 됩니다. 변경되야 할 인덱스에 해당되는 노드를 찾고 갱신한 뒤, 거슬러 올라가면서 해당 노드의 값들을 갱신합니다.
한 번 수를 바꿀 때(갱신)하는 경우 시간 복잡도는 트리의 높이인 O(lgN)입니다.
이제 수열에서 a~b의 구간 합을 탐색하는 방법을 알아봅시다.

노드(s~e)에서 탐색할 때 나오는 경우의 수는 다음과 같습니다. [그림 2] 참고.
1. 노드(s~e)가 구간(a~b)을 일부 포함
노드 1~4에서 3~4만 필요한 값입니다.
따라서 원하는 값만을 가져오기 위해서 자식노드들을 탐색해야 합니다.
2. 노드(s~e)가 구간(a~b)를 완전 포함
1번과 마찬가지로 필요한 부분(3~5)과 필요 없는 부분(2)을 구분해야 합니다.
따라서 필요한 값을 찾기 위해 자식 노드들을 탐색합니다.
3. 노드(s~e)가 구간(a~b)에 포함되지 않음
이 경우 해당 노드는 우리한테 필요없는 값입니다.
따라서 우리가 원하는 값이 없으므로 0을 리턴합니다.
4. 노드(s~e)가 구간(a~b)에 완전 포함됨
이 경우에는 노드가 통째로 필요한 값이므로 더 이상 탐색할 필요도 없이 곧바로 사용하면 됩니다.
해당 노드 값을 리턴합니다.
이제 아까 만들었던 세그먼트 트리를 이용해서 3~5 구간 합을 구해봅시다.

이진 탐색 트리처럼 탐색의 시작은 루트 노트입니다.
루트 노드가 가지고 있는 합의 구간은 1~5입니다. 그런데 저희는 지금 3~5를 구하고 싶습니다.
1~2는 필요가 없는 값이고 3~5는 필요한 값인데 이를 현재 노드에서는 구하고자 하는 값만을 가져올 수가 없습니다. 즉, 어떤 수가 우리가 사용해야 하는 값인지 모릅니다. [2]
그러므로 자식 노드로 내려가서 필요한 값만을 가지고 오는 작업이 필요합니다

트리의 레벨 1로 내려왔습니다. 이제 각 노드들을 봅시다.
1~3의 구간합은 아까와 같이 일부는 필요하고 일부는 필요없는 값입니다. 따라서 마찬가지로 자식노드들을 탐색하러 내려가야 합니다. [1]
4~5 구간합을 봅시다. 저희가 구해야 하는 범위가 3~5이므로 4~5는 모두 필요한 값이네요. 따라서 해당 노드 값 9를 반환해줍니다. [4]

아까 1~3 노드에서 필요한 값만을 구하기 위해 자식 노드로 내려왔었습니다. 해당 자식 노드들을 봅시다.
1~2의 구간 합은 저희가 구하고자 하는 값과 교집합이 하나도 없네요. 즉, 우리가 필요한 값이 하나도 없다는 뜻으로 0을 리턴해줍니다.[3]
3 노드는 저희가 필요한 값입니다. 따라서 해당 노드 값 3을 리턴해줍니다. [4]

따라서 1~3노드가 왼쪽 자식에서 0, 오른쪽 자식에서 3을 받아왔습니다.
즉, 두 수를 더한 값, 3이 우리가 필요한 값이 됩니다. 이를 다시 부모 노드로 반환해줍니다.

1~5 노드는 왼쪽 자식에서 3, 오른쪽 자식에서 9를 받아와서 총 12가 우리가 필요한 값이 됩니다.
현재 노드는 루트이므로 모든 수열에서 3~5 구간 합을 구했다는 것을 알 수 있습니다. 즉, 루트 노드에서 반환된 12가 수열 A에서 인덱스 3~5의 구간합 입니다.
원하는 구간 합을 구하는(탐색하는) 시간 복잡도는 O(lgN)입니다.

세그먼트 트리는 만약 수열의 크기가 2의 제곱형태라면 트리의 마지막 레벨의 노드도 모두 찬 포화 이진 트리가 되고, 2의 제곱형태가 아니라면 마지막 레벨을 제외한 모든 레벨의 노드가 가득 찬 이진 트리가 됩니다.
이진 트리의 값을 저장할 때 배열을 사용하면 노드 인덱스가n일 때, 왼쪽 자식은2n, 오른쪽 자식은 2n+1이 되므로 인덱스로 트리 노드 값에 접근이 쉽습니다.
따라서 비록 트리가 포화 이진 트리가 아니여서 메모리 낭비가 있다고 하더라도 배열을 이용하는 것이 구현에 쉽습니다.

그러면 트리 배열의 크기는 얼마로 해야 될까요.
수열의 크기를 N이라고 했을 때, 세그먼트 트리의 높이 H는 log2N을 소수점 첫째 자리에서 올림해준 값과 같습니다. 포화 이진트리에서 노드 개수는 2(트리 높이+1)-1 입니다. 따라서 [그림 3]과 같은 경우 배열의 크기를 15로 만들어주면 세그먼트 트리를 모두 저장할 수 있습니다.
세그먼트 트리를 이용해서 구간 합을 구하는 문제입니다.
구간 합 구하기(2042) :https://www.acmicpc.net/problem/2042
참고 :https://www.acmicpc.net/blog/view/9
'알고리즘 이론' 카테고리의 다른 글
| 크루스칼 알고리즘(Kruskal’s algorithm) (0) | 2020.02.06 |
|---|---|
| 프림 알고리즘(Prim's algorithm) (0) | 2020.02.06 |
| 트리 순회(전위 순회, 중위 순회, 후위 순회) (2) | 2019.10.04 |
| 벨만포드 알고리즘 (Bellman-Ford algorithm) (0) | 2019.09.26 |
| [알고리즘] 대회 TIP (for me) (0) | 2019.09.23 |



댓글