트리를 배우면 같이 배우게 되는 개념 중 하나죠. 트리 순회에 대해 알아보겠습니다.
트리 순회에는 전위 순회(preorder), 중위 순회(inorder), 후위 순회(postorder) 가 있습니다.
텍스트 추가
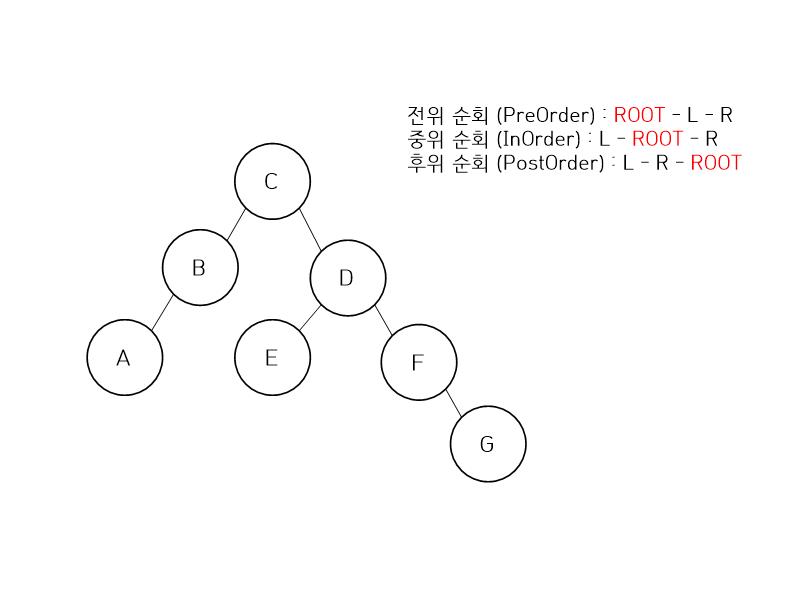
[그림 1]은 예시로 그린 트리 입니다.
전위 순회는 [루트 - 왼쪽 자식 - 오른쪽 자식] 순으로 순회합니다.
중위 순회는 [왼쪽 자식 - 루트 - 오른쪽 자식] 순으로 순회합니다.
후위 순회는 [왼쪽 자식 - 오른쪽 자식 - 루트] 순으로 순회합니다.
이것만 안다면 차근차근 해나가면 됩니다.

일단 전위 순회입니다. 루트 - 왼쪽 - 오른쪽 순으로 순회한다면 결과는 CBAEDFG 가 됩니다.
개인적으로 제일 쉽다고 생각하는 순회방법입니다.
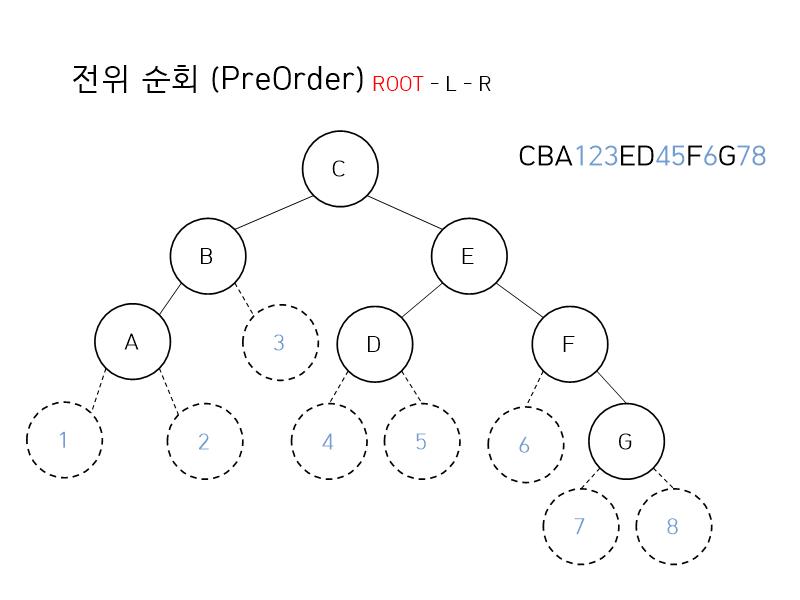
만약 잘 이해가 되지 않는다면 [그림 3]처럼 모든 노드에 왼쪽 자식과 오른쪽 자식을 임의로 그려놓고 탐색해봅시다. 그러면 결과가 CBA123ED45F6G78이 됩니다. 여기서 숫자들을 뺀다면 예시 그래프의 전위 순회 결과가 나오게 되겠죠?

그 다음은 중위 순회 입니다. 왼쪽 - 루트 - 오른쪽 순으로 순회한다면 결과는 ABCDEFG 가 됩니다.

마찬가지로 모든 노드에 왼쪽 자식과 오른쪽 자식이 있다고 생각하고 중위 순회를 한다면
1A2B3C4D5E6F7G8 이 됩니다. 마찬가지로 여기서 숫자를 뺀다면 위에서 구한 중위 순회 결과가 나오게 됩니다.
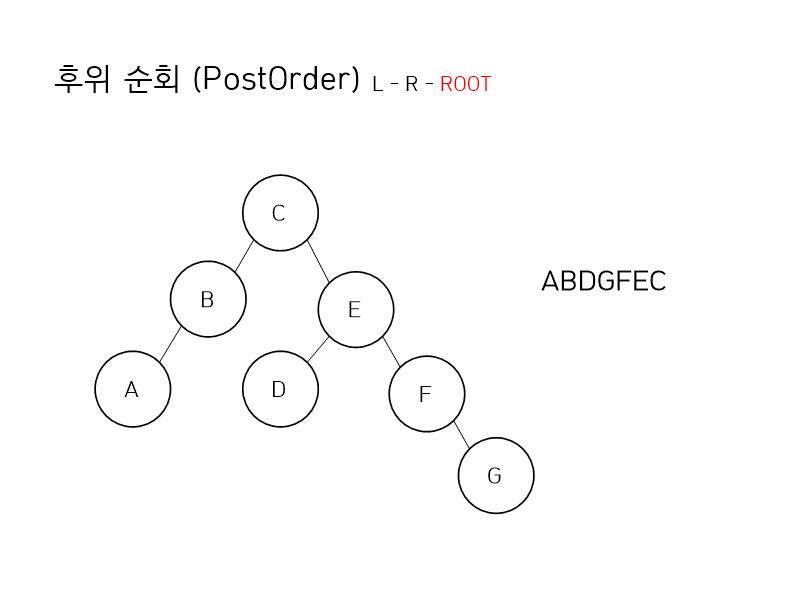
그 다음은 후위 순회 입니다. 왼쪽 - 오른쪽 - 루트 순으로 순회한다면 결과는 ABDGFEC 가 됩니다.

이 또한 모든 노드에 왼쪽 자식과 오른쪽 자식이 있다고 생각하고 후위 순회를 한다면
12A3B45D678GFEC 가 됩니다. 마찬가지로 여기서 숫자를 뺀다면 위에서 구한 후위 순회 결과가 나오게 됩니다.
앞서 말씀드린대로 모든 노드에 왼쪽 자식과 오른쪽 자식이 있다고 생각하는 방법은 굳이 그림처럼 노드를 그려서 숫자까지 적고 할 필요는 없고 간단히 차근차근 노드를 짚어가며 순회하다가 노드가 없으면 적지 않으면 됩니다. 반복하다 보면 쉽게 할 수 있을 것입니다.
사실상 [그림 1]만 기억하면 됩니다.
위의 예시대로 생긴 트리를 만들고 3가지 방법 순회(전위 순회, 중위 순회, 후위 순회) 하는 코드를 작성해 보았습니다.
소스코드 : https://github.com/fpdjsns/Algorithm/blob/master/tip/%ED%8A%B8%EB%A6%AC%EC%88%9C%ED%9A%8C.cpp

'알고리즘 이론' 카테고리의 다른 글
| 프림 알고리즘(Prim's algorithm) (0) | 2020.02.06 |
|---|---|
| 세그먼트 트리(Segment Tree) (0) | 2020.02.02 |
| 벨만포드 알고리즘 (Bellman-Ford algorithm) (0) | 2019.09.26 |
| [알고리즘] 대회 TIP (for me) (0) | 2019.09.23 |
| 다익스트라 알고리즘 (Dijkstra's algorithm) (0) | 2019.09.18 |


댓글