다익스트라는 최단경로 알고리즘입니다.
하나의 특정 도시에서 다른 도시들로가는 최단경로, 최소비용을 구하는데 사용됩니다.
도시 i에서 j로 가는 비용이 arr[i][j]이고 도시들의 방문여부를 배열 check에 저장, 도시로 가는 최소비용을 배열 dist에 저장한다고 했을 때,
다익스트라 알고리즘은 다음과 같습니다.
1. 현재 도시(now)의 방문 여부를 체크합니다. [check[now] = true]
2. 현재 도시(now)를 거쳐 갈 수 있는 도시(next)들의 비용이 현재 저장되어 있는 비용(dist[next])보다 큰 경우 이를 갱신합니다.
[ dist[next] > dist[now] + arr[now][next] => dist[next] = dist[now] + arr[now][next] ]
3. 방문하지 않은 도시들(check[ind] = false 인 ind) 중 비용(dist[ind])이 가장 작은 도시를 방문합니다. 비용이 최소인 도시(min)를 방문하는 이유는 해당 도시들은 다른 도시들을 거치는 경로의 비용으로 갱신되지 않을 것이기 때문에 더 이상 변경이 없는 확정된 비용이기 때문입니다.
(dist[min]은 어떠한 dist[] 보다 작으므로 dist[min] > dist[ind] + arr[ind][min] 를 만족하는 ind는 존재하지 않는다.)
4. 1~3번을 모든 도시를 방문할 때까지 반복합니다.

[그림 1]과 같은 그래프로 다익스트라 알고리즘을 해봅시다.
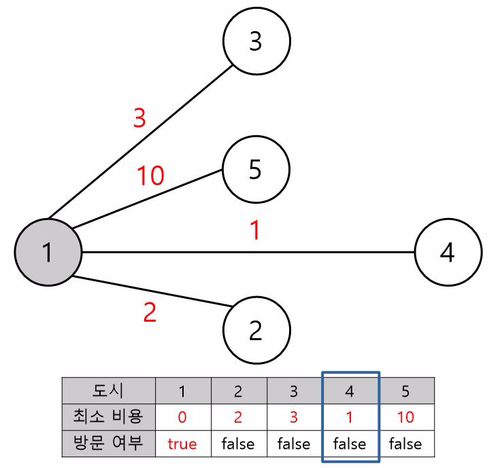
시작도시는 1번으로 하겠습니다.
1번 도시의 최소 비용은 시작 도시이므로 0이 되고 방문 여부를 true로 바꿔줍니다.
1번 도시에서 갈 수 있는 아직 방문하지 않은 도시들은 2,3,4,5번 이고 이들은 아직 최소비용이 없으므로 dist[next] = dist[1] + dist[next] 로 모두 갱신합니다.
아직 방문하지 않은( check[] = false ) 도시들 중 최소 비용이 최소인 도시는 4번 입니다.
따라서 다음은 4번 도시를 방문합니다.

4번 도시의 방문여부를 true로 갱신합니다.
4번 도시에서 아직 방문하지 않은 도시들의 비용을 갱신해봅시다.
4번 도시에서 갈 수 있는 도시들은 1,2,3,5입니다. 이 중 1번 도시는 이미 방문을 했으므로 제외하고 2,3,5 번 도시의 최소 비용을 살펴봅시다.
4번 도시를 거쳐서 next 도시를 가는 비용은 dist[4] + arr[4][next] 입니다.
2번 도시 : 4번 도시를 거쳐가는 비용(1 + 2 = 3)은 현재 2번 도시로 가는 비용(dist[2] = 2) 보다 크므로 갱신할 필요가 없습니다.
3번 도시 : 4번 도시를 거쳐가는 비용(1 + 1 = 2)은 현재 3번 도시로 가는 비용(dist[3] = 3) 보다 작으므로 2로 갱신해줍니다.
5번 도시 : 4번 도시를 거쳐가는 비용(1 + 3 = 4)는 현재 5번 도시로 가는 비용(dist[5] = 10) 보다 작으므로 4로 갱신해줍니다.
최소 비용이 가장 작은 도시가 2, 3번 도시인데 이 중 어느 도시를 먼저 방문하든지 상관없습니다.
저는 2번 도시를 다음으로 방문해 보겠습니다.

2번 도시의 방문 여부를 true로 갱신합니다.
2번 도시에서 갈 수 있는 도시들은 1, 4번 도시인데 이들 모두 방문을 이미했으므로 최소 비용의 갱신은 할 필요가 없습니다.
방문하지 않은 도시들 중 최소 비용이 최소인 3번 도시를 다음에 방문합니다.
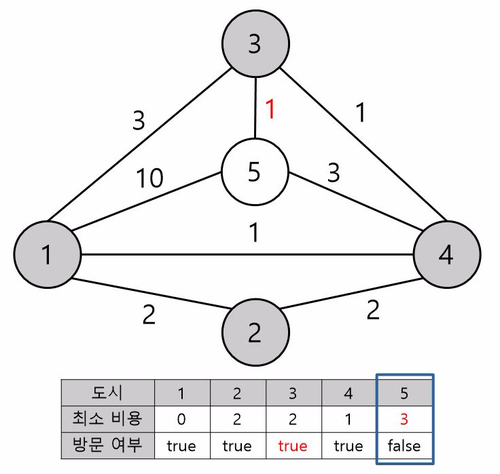
3번 도시의 방문 여부를 true로 갱신합니다.
3번 도시에서 아직 방문하지 않은 도시들의 비용을 갱신해봅시다.
3번 도시에서 갈 수 있는 도시들은 1,4,5입니다. 이 중 1, 4번 도시는 이미 방문을 했으므로 제외하고 5 번 도시의 최소 비용을 살펴봅시다.
3번 도시를 거쳐서 next 도시를 가는 비용은 dist[3] + arr[3][next] 입니다.
5번 도시 : 3번 도시를 거쳐가는 비용(2 + 1 = 3)은 현재 5번 도시로 가는 비용(dist[5] = 4) 보다 작으므로 3으로 갱신해줍니다.
방문하지 않은 도시들 중 최소 비용이 최소인 5번 도시를 다음에 방문합니다.

5번 도시의 방문여부를 true로 갱신합니다.
모든 도시들을 방문했으므로 종료합니다.
dist 배열을 통해 1번도시를 시작도시로 했을 때 다른 도시들로 가는 최소비용을 알 수 있습니다.
간선의 개수가 E일 때, 해당 정점과 연결된 간선들을 탐색 시, 우선순위 큐에서 간선 정보를 가져옵니다. 우선순위큐에 들어가는 간선 정보는 E개고 모든 간선들을 탐색하므로 시간복잡도는 O(ElogE)입니다.
+ 간선의 가중치가 양수여야 하는 이유
다익스트라는 모든 간선의 가중치가 양수인 경우만 사용됩니다.
다음 정점 선택 시 dist 배열에서 가장 작은 비용(최단거리, min)을 선택하는데 이는 dist[min]이 다른 정점을 지나서 방문했을 때의 비용 즉, dist[now] + weight가 dist[min] 보다 작아질 수 없기 때문입니다. (dist[min] < 모든 dist[now] 이므로 dist[min] > dist[now] + weight이 나올 수 없음)
만약 가중치가 음이라면(weight가 -가 될 수 있다면) dist[min] > dist[now] + weight이 나올 수 없다는 다익스트라의 가정이 무너집니다.
따라서 간선의 가중치가 음수가 있는 경우 다익스트라 알고리즘은 사용할 수 없습니다.
간선의 가중치가 음수라면 다익스트라가 아닌 벨만포드 알고리즘을 사용합니다.
이는 다른 포스팅에서 설명하겠습니다.
최단경로 알고리즘을 이용하는 문제입니다.
최소비용 구하기 (1916) : https://www.acmicpc.net/problem/1916
'알고리즘 이론' 카테고리의 다른 글
| 벨만포드 알고리즘 (Bellman-Ford algorithm) (0) | 2019.09.26 |
|---|---|
| [알고리즘] 대회 TIP (for me) (0) | 2019.09.23 |
| 외판원 순회(TSP: Traveling Salesperson Problem) (8) | 2019.08.31 |
| 너비 우선 탐색(BFS: Breadth First Search) (0) | 2019.08.28 |
| 버블 정렬(Bubble Sort) (0) | 2019.06.12 |


댓글