최장 감소 수열 (LDS: Longest Decreasing Sequence)과 최장 증가 수열(LIS: Longest Increasing Sequence)에 대해 알아보겠습니다.
저는 코드를 최장 감소 수열에 대해서 짰기 때문에 최장 감소 수열을 설명하겠습니다. 최장 증가 수열과 최장 감소 수열은 증가하느냐 감소하느냐의 차이 밖에 없으므로 코드를 짤 때도 부등호 하나의 차이밖에 나지 않으므로 LDS만 이해한다면 LIS 또한 이해할 수 있을 것입니다.
최장 감소 수열이란 가장 긴 감소하는 부분 수열을 말합니다. 예를 들어서 살펴보도록 하겠습니다.
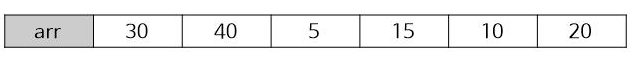
위와 같이 30, 40, 5, 15, 10, 20인 수열이 존재한다면 이 수열에 대해서 최장 감소 수열은

40, 15, 10이 됩니다. 사실 코드를 어떻게 짜느냐에 따라 30, 15, 10 또한 정답이 될 수 있습니다.
저는 40, 15, 10이 정답이 되는 알고리즘에 대해 설명하겠습니다.

LDS를 구현하기 위해서는 우선 1차원 배열이 하나 필요합니다. 그리고 arr배열을 앞에서 부터 탐색하면서 하나씩 d배열에 넣습니다. 우선 d가 비어있으므로 d의 첫 번째 자리에 30을 넣습니다.

그 다음부터는 들어오는 값보다 작거나 같은 값이 있으면 해당 위치에 값을 갱신하고, 들어오는 값이 가장 작은 경우에는 배열의 맨 뒤에 저장해줍니다.
30은 40보다 작으므로 30 자리에 40을 갱신시킵니다.

배열 d에 5보다 작은 수는 없으므로 배열의 끝에 5를 넣습니다.

5는 15보다 작으므로 5의 위치에 15를 갱신시킵니다.

배열 d에 10보다 작은 수는 없으므로 배열의 끝에 10을 넣습니다.

15는 20보다 작으므로 15의 위치에 20을 갱신시킵니다.
모든 데이터를 처리하였으므로 완성된 d 배열은 위와 같습니다.
따라서 최장 감소 수열의 길이는 배열 d의 길이인 3이 됩니다.
(23.07.30) 위와 같은 방법으로 구한 d 배열로는 최장 감소/증가 수열의 길이는 구할 수 있으나 배열안의 요소가 갱신되는 식이므로 명확한 배열을 구할 수는 없습니다. 따라서 아래에서 설명한 최장 감소 수열의 명확한 요소들을 구하는 방법은 잘못된 방법입니다.
그런데 먼저 알아보았던 최장 감소 수열과 완성된 d의 수열은 다릅니다. d배열은 최장 감소 수열의 길이를 알아보기 위해서 사용하는 배열일 뿐 최장 감소 수열에 대해서는 또 다른 과정이 필요합니다.
d배열에서 최장 감소 수열의 일부분은 가장 마지막 데이터인 '10'입니다. 이 데이터를 가지고 역으로 arr배열을 거슬러 올라가서 최장 감소 수열을 구합니다.

일단 d 배열의 마지막 원소인 10은 arr배열의 5번째 원소입니다. 이 위치에서 앞으로 가면서 수를 비교 해서 최장 감소 수열을 구합니다. 이 때, 거꾸로 탐색하므로 더 큰 수를 찾아야 합니다.
4번째 원소인 15는 10보다 크니까 최장 감소 수열이 될 수 있습니다. 이제 15보다 큰 수를 찾습니다.
3번째 원소인 5는 15보다 작아서 최장 감소 수열이 될 수 없습니다.
2번째 원소인 40은 15보다 크니까 최장 감소 수열이 될 수 있습니다. 이제 40보다 큰 수를 찾습니다.
1번째 원소인 30은 40보다 작아서 최장 감소 수열이 될 수 없습니다.
arr의 시작지점까지 최장 감소 수열을 찾아보면 10, 15, 40이 나옵니다. 역추적한 결과이기 때문에 reverse한 값을 출력해주면 40, 15, 10이 최장 감소 수열인 것을 확인할 수 있습니다.

위의 예시로 최장 증가 수열(LIS)를 만들기 위해서 배열 d를 채워본다면 위와 같이 나옵니다.
들어오는 값보다 크거나 같은 값의 위치에 갱신하거나 들어오는 값이 배열 d에 있는 모든 수보다 크다면 배열의 뒤에 넣어주면서 d를 완성시키면 됩니다.
최장 증가 수열을 구할 때도 배열 d의 마지막 수인 20부터 역추적하여 구합니다.
LIS와 LDS를 사용하여 푸는 가장 기본적인 문제입니다.
가장 긴 증가하는 부분 수열(11053) : https://www.acmicpc.net/problem/11053
가장 긴 감소하는 부분 수열(11722) : https://www.acmicpc.net/problem/11722
최장 감소 수열을 코드로 작성해보았습니다.
데이터 수(n)를 입력받고 n개의 데이터를 입력받습니다.
그리고 입력받은 수열에 대한 최장 감소 수열의 길이와 최장 감소 수열을 출력합니다.
최장 증가 수열은 코드에서 조건문의 부등호만 적절히 바꿔주면 됩니다.
저는 간단하게 들어오는 값보다 작거나 같은 값의 위치 찾는 것을 배열의 앞에서 부터 차례대로 탐색해서 찾아 주었는데, 이 부분을 이분탐색으로 구현하면 빠르게 검색하여 시간복잡도를 줄일 수 있습니다.
소스코드 : https://gist.github.com/fpdjsns/cf87f185e5556852f197cc6c95a381c3
'알고리즘 이론' 카테고리의 다른 글
| 너비 우선 탐색(BFS: Breadth First Search) (0) | 2019.08.28 |
|---|---|
| 버블 정렬(Bubble Sort) (0) | 2019.06.12 |
| 힙 정렬(Heap sort) (0) | 2019.05.30 |
| 퀵 정렬(QuickSort) (0) | 2019.05.07 |
| 병합 정렬 (Merge Sort) (0) | 2019.04.23 |




댓글