병합 정렬은 분할 정복(Divide & Conquer)의 대표적인 예로 배열을 잘게 나누어서 다시 합칠 때 정렬하는 방법입니다.
{8, 4, 6, 2, 1, 3, 5, 9, 10, 7} 인 배열을 병합 정렬 보겠습니다.

크기가 1인 배열이 될 때 까지 반으로 분할 하고, 이를 다시 합치면서(정복) 정렬하는 것이 병합 정렬입니다.
합치면서 정렬하는 방법에 대해 좀 더 상세히 알아보도록 하겠습니다.

배열 A : {4, 8} 과 B: {1, 2, 6}을 합쳐보도록 하겠습니다.
일단 배열의 크기가 1일 때부터 정렬하면서 합쳐주었으므로 배열 {4, 8}과 {1, 2, 6}은 정렬된 상태입니다. 그러므로 가장 앞에 수가 최솟값입니다.
각 배열을 인덱스 0부터 비교해가면서 작은 값을 배열의 0번째 값에 넣어줍니다.
위의 그림을 보면 4(A[0]) 보다 1(B[0])이 더 작으므로 1을 인덱스 0에 넣어줍니다.

배열 B의 0번째 값은 이미 배열에 넣었으므로 다음 값과 A[0]을 비교합니다.
4(A[0]) > 2(B[1]) 이므로 2를 배열에 넣어줍니다.

마찬가지로 B[1]은 배열에 이미 넣었으므로 다음 값과 A[0]을 비교합니다.
4(A[0]) < 6 (B[2]) 이므로 4를 배열에 넣어줍니다.

A[0]은 배열에 이미 넣었으므로 A[1]과 B[2]를 비교합니다.
8(A[1]) > 6(B[2]) 이므로 6을 배열에 넣습니다.

B[2]를 배열에 넣었으므로 B[3]을 비교대상으로 사용하여야 하는데 B[3]은 B 배열의 범위를 넘어갑니다.
따라서 이후 부터는 비교하지 않고 아직 배열에 넣지 않은 배열 A 값들을 모두 배열에 넣어주면 됩니다.
이번에는 {1,2,4,6,8} 과 {3,5,7,9,10} 으로 한 번 더 살펴보겠습니다.
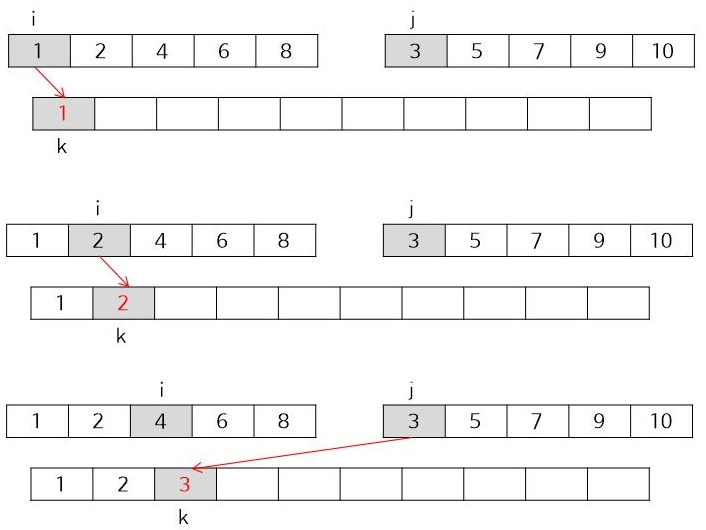



8까지 배열에 넣었으면 배열 A를 모두 사용한 것이 되므로 아직 배열에 넣지 않은 배열 B의 값(9, 10)을 마저 배열에 넣어줍니다.

정렬하고자 하는 배열의 크기를 N이라고 할 때 시간복잡도를 구해봅시다.
배열의 크기가 1/2로 분할될 때의 시간복잡도는 수식이므로 O(1)입니다. 배열의 크기는 아래로 갈수록 1/2씩 작아져서 이를 log2N번 한다고 볼 수 있습니다. 따라서 분할 시 시간복잡도는 O(1) x log2N 입니다.
합칠 때 배열크기 만큼의 시간이 소요되는데 단계별로 합쳐지는 배열들의 크기를 모두 합치면 N입니다. 따라서 단계별로 시간복잡도는 O(N)입니다. 마찬가지로 이를 log2N번 하므로 정복 시 시간복잡도는 O(N) x log2N 입니다.
따라서 병합 정렬 전체 시간 복잡도는 O(log2N) + O(Nlog2N) = O(Nlog2N) 입니다.
배열 크기와 배열안에 들어갈 숫자들을 입력받고 이를 병합 정렬한 결과를 출력하는 소스코드를 작성하였습니다. 참고해 주세요.
소스코드 : https://gist.github.com/fpdjsns/b8680ac12b4474899db0fc4d501e7966
병합 정렬(Merge Sort)
병합 정렬(Merge Sort). GitHub Gist: instantly share code, notes, and snippets.
gist.github.com

'알고리즘 이론' 카테고리의 다른 글
| 힙 정렬(Heap sort) (0) | 2019.05.30 |
|---|---|
| 퀵 정렬(QuickSort) (0) | 2019.05.07 |
| 삽입 정렬 (Insertion Sort) (0) | 2019.04.18 |
| 선택 정렬 (Selection Sort) (0) | 2019.04.15 |
| 허프만 코드(Huffman code) (4) | 2018.10.29 |




댓글