[Leetcode] 629. K Inverse Pairs Array

문제 : https://leetcode.com/problems/k-inverse-pairs-array/

---

inverse pairs : 0 <= i < j < nums.length and nums[i] > nums[j] 조건을 만족하는 [i, j]. 

DP[n][k] = n 크기의 nums 배열이 있을 때 k 개의 inverse pairs 를 가지는 경우의 수.

 

n-1 크기의 nums에서 어떻게 n 크기의 nums를 만들 수 있는지 먼저 살펴보자.

[그림 1]

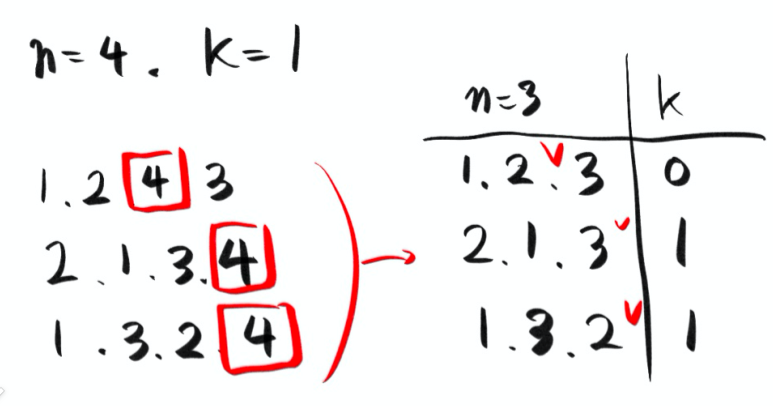
[그림 1] 에서 n=4, k=1인 경우는 왼쪽 아래와 같이 총 3가지 방법이 있다.

3가지 리스트들에서 4인 원소들을 제거하면 오른쪽과 같은 리스트들이 나온다.

여기에서 추론 가능한건 n-1 크기의 배열에서 추가되는 4의 위치에 따라 k(inverse pairs)의 크기가 달라진다는 것이다.

 

[그림 2]

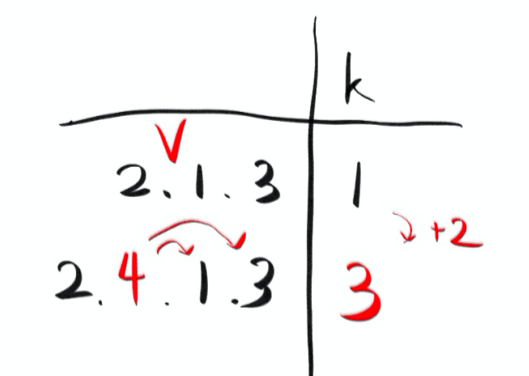
예를 들어보자. [그림 2] 에서 [2, 1, 3] 리스트에서 뒤에서 두 번째 위치에 4를 넣어 [2, 4, 1, 3] 리스트를 만들어보자.

기존 리스트([2,1,3])의 inverse pairs는 1이다. 새로 추가되는 4는 가장 큰 수이기 때문에 4 뒤에 있는 원소들의 수만큼 inverse pairs들이 생긴다. [그림 2] 에서는 [4, 1], [4, 3] 이 추가되어 총 3이 되는걸 확인할 수 있다.

 

즉, dp[n][k] 리스트들에서 n+1 원소를 추가할 때 어디 위치에 추가하냐에 따라서 k가 달라진다.

예를 들어, 뒤에서 4번째 위치에 원소를 추가한다면 dp[n+1][k+4]에 dp[n][k]를 더해주어야 한다는 뜻이된다.

 

기본 아이디어는 위와 같고, DP를 어떻게 채우는지는 https://leetcode.com/problems/k-inverse-pairs-array/discuss/2293243/DP-algo-explained-with-figures-Python 링크 참조.

 

시간/공간복잡도는 O(NK)

---

소스코드 : https://github.com/fpdjsns/Algorithm/blob/master/leetcode/hard/629.%20K%20Inverse%20Pairs%20Array.cpp

---

까먹기 전에 아이디어만 간단히. 역시 DP 난이도가 천차만별이구만. DP 문제인걸 알아도 점화식 생각해내는데 시간이 오래걸렸다.