문제 : https://leetcode.com/problems/search-a-2d-matrix-ii/
m x n 정수형 배열에서 target 이 존재하는지 유무를 반환하라. 배열은 각 행, 열에서 오름차순 정렬되어 있다.
가장 쉽게 생각할 수 있는건 각 행, 혹은 열마다 차례대로 이분탐색을 돌려서 target 값이 있는지 확인한다. 시간복잡도는 O(N logM) or O(M logN).
각 행, 열에서 오름차순 정렬되어 있다는 특징을 독립적으로 보지 않고 탐색조건에 같이 사용할 수 있을지 생각해보았다.

예제 1번의 배열모습이다. x = 1, y = 1 일 때, matrix[x][y]는 5이다. 이때 matrix[x~][y~] 배열을 한 번 보자. 각 행, 열들은 오름차순 정렬되어있으므로 항상 최상단좌측 배열값은 해당 배열의 최소값이다. 이 특징을 이용해서 최상단 좌측 배열값을 찾는 방식으로 target 값을 찾아보자.
x의 초기값을 0, y의 초기값을 n-1로 세팅한다. 이제 x를 증가시키거나 y를 감소시켜 target 값을 탐색한다.
만일 matrix[x][y]가 target이라면 true를 반환한다.
만일 matrix[x][y]가 target보다 작다면 matrix[x~m][y~n] 배열안에 target값이 있을 수 있다는 이야기인데 y를 감소시키며 matrix[x~m][y+1~n] 에는 target 값이 없다는게 판명되었으므로 target 값이 있을 수 있는 곳은 matrix[x~m][y] 이다. 따라서 y값은 고정이 되고 x를 1증가한다.
만일 matrix[x][y]가 target보다 크다면 아직 matrix[x~m][y~n] 배열안엔 target 값이 없으므로 y를 1감소시켜 matrix[x~m][y~n] 범위를 넓혀준다.
위 방법으로 x, y가 matrix 인덱스 범위를 넘어갈때까지 탐색하였는데 target을 발견하지 못하였으면 target이 배열안에 없는 경우이다.

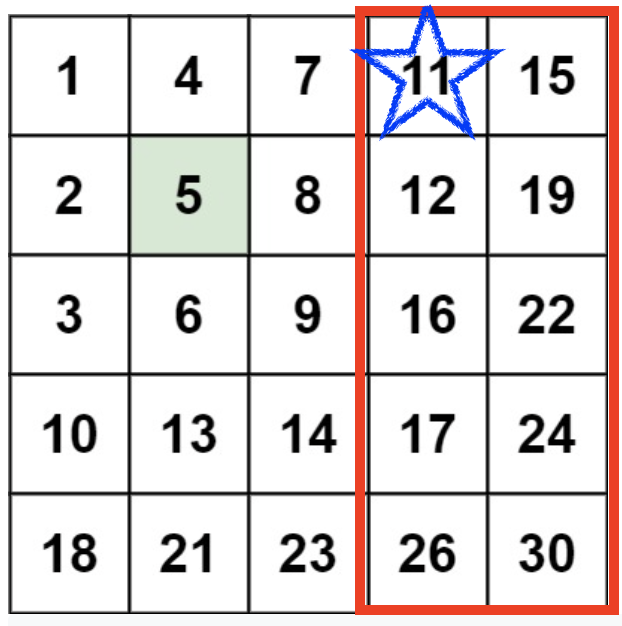



예시 1을 해당 알고리즘으로 탐색하면 위와 같이 x, y인덱스가 갱신된다.
시간복잡도는 O(N+M).
'알고리즘 문제 > Leetcode' 카테고리의 다른 글
| [Leetcode] 289. Game of Life (0) | 2021.11.23 |
|---|---|
| [Leetcode] 106. Construct Binary Tree from Inorder and Postorder Traversal (0) | 2021.11.21 |
| [Leetcode] 461. Hamming Distance (0) | 2021.11.19 |
| [Leetcode] 448. Find All Numbers Disappeared in an Array (0) | 2021.11.18 |
| [Leetcode] 668. Kth Smallest Number in Multiplication Table (0) | 2021.11.16 |
댓글