유니온 파인드(Union-Find)는 집합을 표현하기 위한 자료구조입니다.

이를 표현하기 위해 트리에서 부모노드를 저장하는 배열을 만듭니다.
부모노드가 없는 루트노드인 경우는 자기자신을 저장합니다.
이때 최상위 부모노드가 같은 값들이 같은 집합에 속하게 됩니다. [그림 1]에서는 1, 2, 3이 같은 집합. 4, 5가 같은 집합입니다.
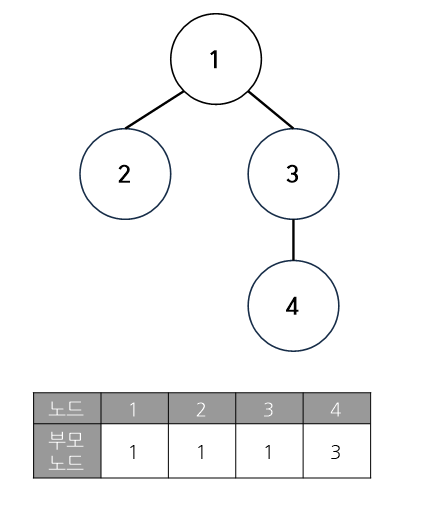
주의할 점은, 부모노드가 아닌 최상위 부모노드가 같은 노드들이 같은 집합에 속합니다.
[그림 2]에서 노드 4와 노드 2는 모두 같은 집합에 속하지만 부모노드 배열만 봐서는 같은 집합에 속하는지 알 수 없습니다. 같은 집합에 속하는지 알기 위해서는 각 노드들의 최상위 부모노드 배열을 알아야 합니다.
노드 4의 부모노드는 3이지만 최상위부모노드는 1이 됩니다. 다른 노드들의 최상위 부모노드도 모두 1이 되므로 같은집합에 속하게 됩니다.
같은 집합에 속하는 두 개의 노드들에 대한 정보가 주어질 때, 이를 [그림 1]과 같은 트리형태로 만들고 부모노드 배열을 만들어야 합니다.
이를 위해, 파인드(Find), 유니온(Union) 2가지 연산을 알아야 합니다.
파인드(Find) 연산
노드 x의 최상위 부모노드를 구하는 연산입니다.

[그림 3]와 같은 경우, 3 노드의 최상위 노드는 1이 됩니다.
fun Find(x):
if(부모노드[x] == x) // 자기자신
return x
return Find(부모노드[x])수도코드로 간단히 표현하면 위와 같습니다.
[그림 3]에서 3 노드의 최상위 부모노드를 찾을 때, 부모노드[3] = 2가 되고 이는 자기자신이 아니기 때문에 루트노드가 아닙니다. 따라서 이번에는 노드의 2의 부모노드를 찾습니다.
부모노드[2] = 1이 되고 이번에는 1의 부모노드를 찾습니다.
부모노드[1] = 1 이므로 1은 루트노드입니다. 즉, 노드 3의 최상위 부모노드는 1이 됩니다.
하나의 노드의 부모노드를 찾는데 총 3번의 부모노드를 탐색했습니다.

그럼 만약 [그림 4]과 같이 n개의 노드들이 위와 같은 트리구조로 되어있다고 가정해봅시다.
노드 n의 최상위 노드를 구하기 위해서는 대략 n번을 탐색하게 됩니다. (시간탐색도 = O(n))
n이 커질수록 시간은 선형적으로 증가할 것이고 n이 크다면 시간이 오래걸려 문제가 발생할수도 있습니다.
이를 방지하기 위해 Find 함수에서 부모노드 배열 값을 부모노드가 아닌 최상위 노드로 갱신해줍니다.
fun Find(x):
if(부모노드[x] == x) // 자기자신
return x
return 부모노드[x] = Find(부모노드[x]) // 갱신수도코드로 나타내면 위와 같습니다.

부모노드배열을 계속 갱신해나가면 트리는 [그림 5]와 같은 구조가 되고, 시간복잡도는 노드의 수와 관계없이 O(1)이 됩니다.
유니온(Union) 연산
두 집합을 합치는 연산입니다.
노드 u, v가 서로 다른 집합에 속해있을 때, 이들 두 집합을 합쳐봅시다.

집합은 [그림 6]와 같습니다. 노드 u를 3, v를 5라고 합시다.
먼저 각 노드들이 어느 집합에 속하는지 알기 위해 Find연산을 해서 최상위 부모노드들을 가져옵니다.
노드 3의 최상위부모노드는 1. 노드 5의 최상위부모노드는 4입니다.
이 두 노드 중 하나의 노드의 부모노드를 또다른 노드로 갱신한다면 하나의 노드가 됩니다.

저는 노드 4의 부모노드를 1로 갱신해보겠습니다.
그럼 최종 트리 구조는 [그림 7]과 같아지고 Find 연산을 이용해 최상위 부모노드를 구하면 모두 1이 나오므로 같은 집합에 속하는 것을 확인할 수 있습니다.
fun Union(int u, int v){
u = Find(u)
v = Find(v)
// 같은 집합인 경우
if(u == v)
return false // 같은 집합이라 Union 연산을 하지 않았음을 반환
// 다른 집합인 경우
부모노드[v] = u; // 부모노드 갱신
return true // 두 집합을 합쳤음을 반환
} 수도코드로 Union 연산을 나타내면 위와 같습니다.
Union 연산의 시간복잡도는 Find 연산의 시간복잡도를 O(1)이라 가정했을 때, O(1)이 됩니다.
유니온 파인드는 크루스칼 알고리즘 구현 시에도 유용하게 사용됩니다.
Union-Find 를 사용한 문제입니다.
[leetcode] 547. Number of Provinces: https://leetcode.com/problems/number-of-provinces/description/
소스코드 : https://github.com/fpdjsns/Algorithm/blob/master/tip/Union-Find.cpp
'알고리즘 이론' 카테고리의 다른 글
| Python 문법 정리 (0) | 2021.09.25 |
|---|---|
| 투포인터 (Two pointer) (0) | 2021.09.12 |
| 플로이드 워셜 알고리즘 (Floyd warshall) (0) | 2021.06.13 |
| 트리의 지름 (0) | 2021.02.21 |
| [C++/STL] stack을 vector로 변환하기 (0) | 2021.01.21 |

댓글