[Leetcode][1074] Number of Submatrices That Sum to Target

문제 : leetcode.com/problems/number-of-submatrices-that-sum-to-target/

---

2차원 배열 matrix와 target 정수가 주어진다.

matrix[x][y] (x1 <= x <= x2, y <= y <= y2)의 합이 target이 되는 (x1, y1, x2, y2)집합의 개수를 구하라.

---

부분합 혹은 DP 문제.

matrix[0~i][0~j] 에 해당하는 수의 합을 저장하는 배열 subSum[i][j]를 구한다.

 

[그림 1]

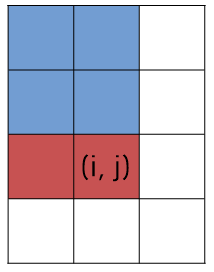
subSum[i][j] = subSum[i-1][j] + matrix[i][0~j]까지의 합 ([그림 1] 참고)

 

문제에서는 x1 <= x, y1 <= y 범위로 표시했지만 부분합에서는 x1 < x, y1 < y 처럼 포함안되는게 계산식이 더 간단하므로 조건을 바꾸고 (x1, y1, x2, y2)에 포함되는 matrix 요소들의 합을 구해보자.

 

[그림 2]

[그림 2]를 보면 우리가 알고싶은 범위는 회색이고. 이는 빨간색 사각형 - 파란색 사각형 + 중복으로 제거된 초록색 사각형 이다.

이를 수식으로 나타내면 다음과 같다.

subSum[x2][y2] - subSum[x2][y1] - subSum[x1][y2] + subSum[x1][y1]

 

matrix에서 나올 수 있는 모든 (x1, x2, y1, y2) 를 탐색하면서 위 수식 결과가 target과 같다면 정답+1을 해준다.

 

시간복잡도는 matrix의 행, 열 크기가 각각 N, M이라 할 때, O(N^2 * M^2).

---

소스코드 : github.com/fpdjsns/Algorithm/blob/master/leetcode/hard/1074.%20Number%20of%20Submatrices%20That%20Sum%20to%20Target.cpp