이진 검색 트리(Binary Search Tree, BST)는 탐색을 효율적으로 할 수 있는 자료구조 중 하나입니다.
이진 검색 트리의 성질은 다음과 같습니다.
- 각 노드에 고유의 값이 있다.
- 노드의 왼쪽 서브트리는 노드 값 보다 작은 값들이다.
- 노드의 오른쪽 서브트리는 노드 값 보다 큰 값들이다.
- 서브트리 또한 이진 검색 트리이다.
생성
노드를 생성하는 방법을 알아보겠습니다.
방법은 우선 첫 번째로 입력받은 수는 루트 노드로 만듭니다.
그 뒤에 입력받는 수는 루트로부터 노드의 수와 비교하여
작으면 왼쪽, 크면 오른쪽 자식 노드로 내려갑니다.
그리고 노드가 없을 때는 해당 위치에 입력받은 값으로 노드를 생성합니다.
예를 들어서 알아봅시다.
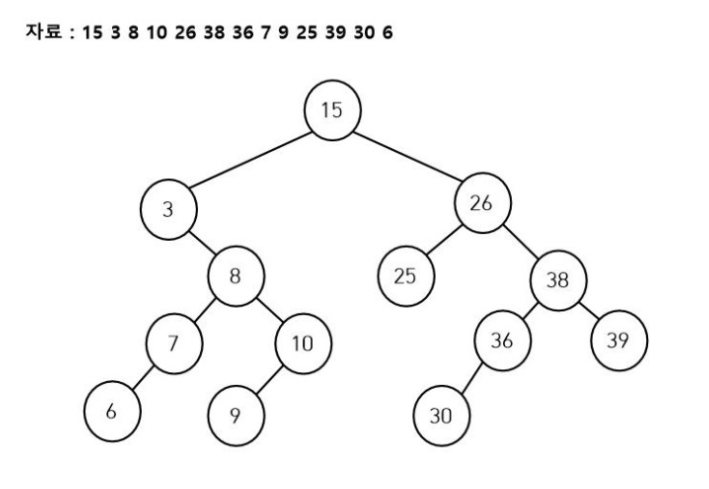
자료 : 15 3 8 10 26 38 36 7 9 25 39 30 6

첫 번째로 입력받는 수이기 때문에 루트 노드로 만들어 줍니다.

3은 15보다 작으므로 왼쪽 자식으로 내려가야 하는데, 15노드의 왼쪽 자식이 없으므로 노드를 생성해 연결해 줍니다.

8은 15보다 작으므로 왼쪽 자식으로 내려갑니다.
8은 3보다 크니까 오른쪽 자식으로 내려가야하는데 오른쪽 자식이 존재하지 않으므로 노드를 생성해서 연결해 줍니다.

[10] [26]
1. 15 > 10 : 왼쪽 1. 15 < 26 : 오른쪽
2. 3 < 10 : 오른쪽 2. 노드 생성
3. 8 < 10 : 오른쪽
4. 노드 생성


탐색
다음으로는 노드를 탐색하는 방법을 알아보겠습니다.
방법은 생성하는 것과 비슷합니다.
찾는 수가
1. 노드와 같으면 탐색 성공
2. 노드보다 작으면 왼쪽
3. 노드보다 크면 오른쪽
4. 노드와 같지 않는데 자식이 존재하지 않는 경우 탐색 실패
이것도 예를 들어서 알아봅시다.
이진 검색 트리는 위에서 만든 트리를 사용하겠습니다.

[13]
1. 15 > 13 : 왼쪽
2. 3 < 13 : 오른쪽
3. 8 < 13 : 오른쪽
4. 10 < 13 : 오른쪽
5. 노드 없음 -> 탐색 실패

[38]
1. 15 < 38 : 오른쪽
2. 26 < 38 : 오른쪽
3. 38 = 38 : 탐색 성공
삭제
다음으로는 노드를 삭제하는 방법을 알아보겠습니다.
노드를 삭제하는 방법은 삭제하고자 하는 노드를 먼저 찾아야 하기 때문에
탐색 연산을 먼저 수행하여 노드를 찾는 것을 먼저 실행합니다.
해당 노드를 찾았다고 했을 때, 노드를 삭제하는 방법은 크게 3가지로 나뉩니다.
삭제하고자 하는 노드가
1. 단노드인 경우
2. 자식이 하나인 경우
3. 자식이 두 개인 경우
차례대로 알아보도록 하죠.
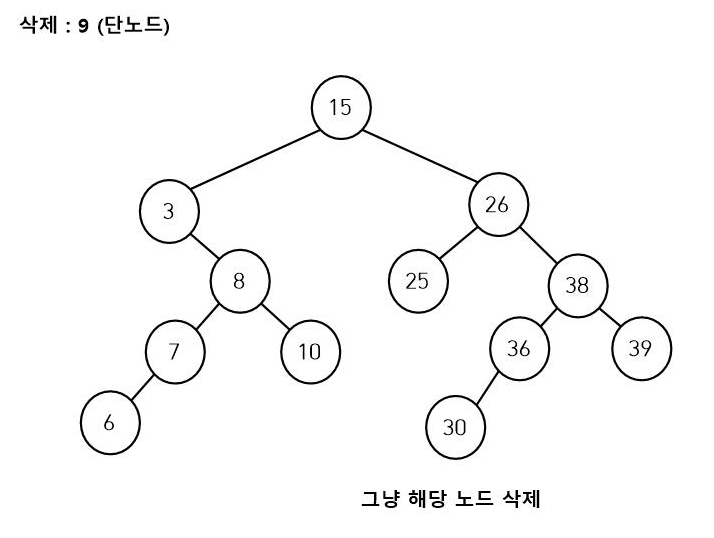
1. 단노드인 경우
탐색하여 찾은 노드를 삭제해주기만 하면 됩니다.
후속 처리가 필요 없기 때문에 가장 간단한 경우입니다.

2. 자식이 하나인 경우
탐색하여 찾은 노드를 삭제한 후
삭제한 노드 위치를 삭제한 노드의 자식 노드로 대체합니다.
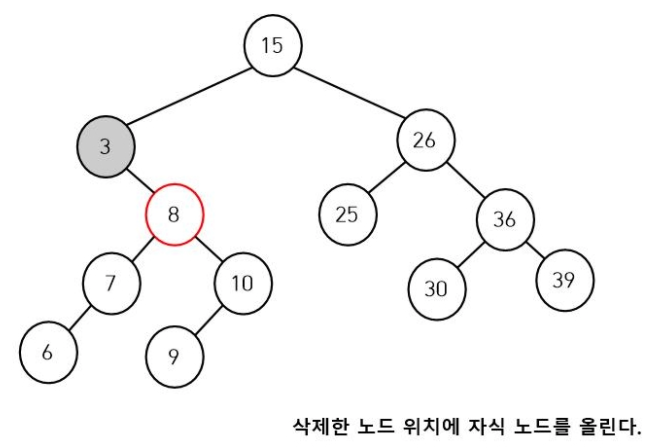
삭제하려는 노드는 3이고 그 자식 노드는 8입니다.
일단 3을 삭제하면 삭제 노드의 부모 노드인 15노드의 왼쪽 자식이 비게 됩니다.
만약 3을 삭제한 뒤 후속 처리를 해주지 않으면 왼쪽 서브트리(6, 7, 8, 9, 10)와의 연결이 끊기게 됩니다.
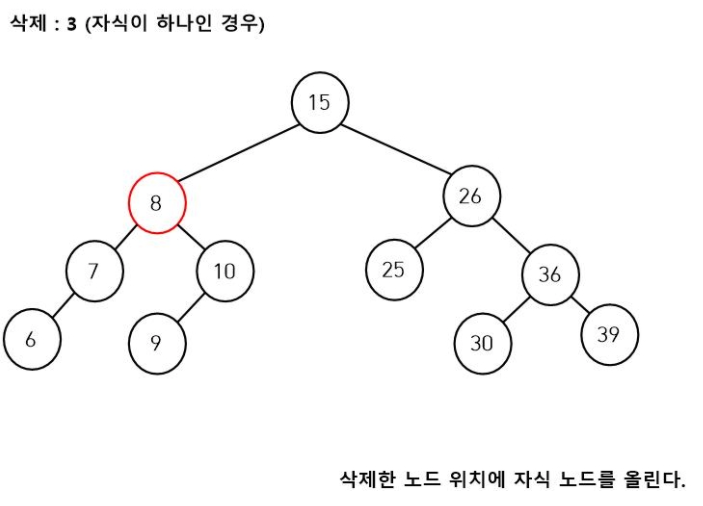
따라서 노드 8(3 자식노드)를 노드 15(3 부모노드)의 왼쪽 자식(노드 3이 부모자식으로 부터 왼쪽 자식으로 연결되어 있었으므로)으로 연결해주는 후속 처리가 필요합니다.
3. 자식이 두 개인 경우
탐색하여 찾은 노드를 삭제한 후
삭제한 노드 위치를 왼쪽 자식 서브트리 혹은 오른쪽 자식 서브트리의 최대값 노드를 올립니다.
왼쪽 서브트리를 사용할지 오른쪽 서브트리를 사용할 지에 따라 트리의 모양은 달라지나 효능은 같으므로 아무거나 선택해도 상관없습니다. 저는 왼쪽 서브트리의 최대값 노드로 삭제 노드를 대체하도록 하겠습니다.
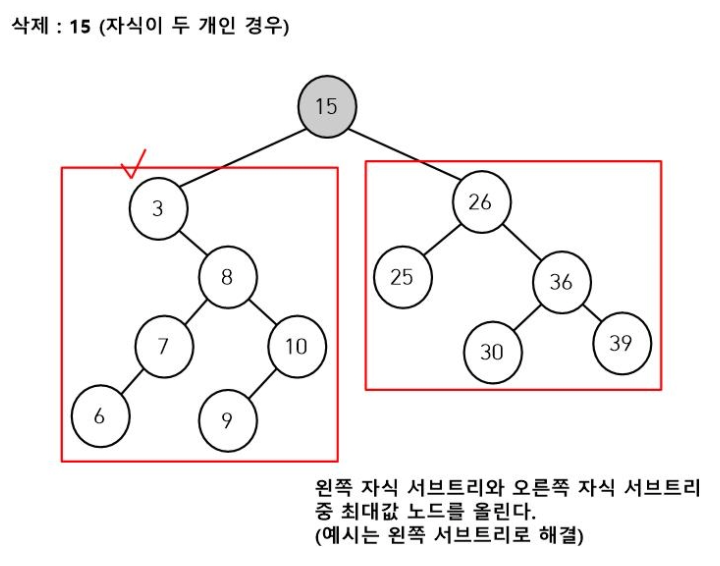
삭제하려는 노드는 15입니다.
자식 노드는 두 개가 있고 그 중 왼쪽 서브트리를 살펴보도록 하겠습니다.

왼쪽 서브트리의 최대값 노드를 찾는 방법은 오른쪽 자식이 존재하지 않을때까지 오른쪽 자식으로 내려갑니다. 오른쪽 자식이 없다면 해당 노드가 최대값입니다.
즉, 위의 상황에서는 노드 10이 왼쪽 서브트리의 최대값 노드입니다.
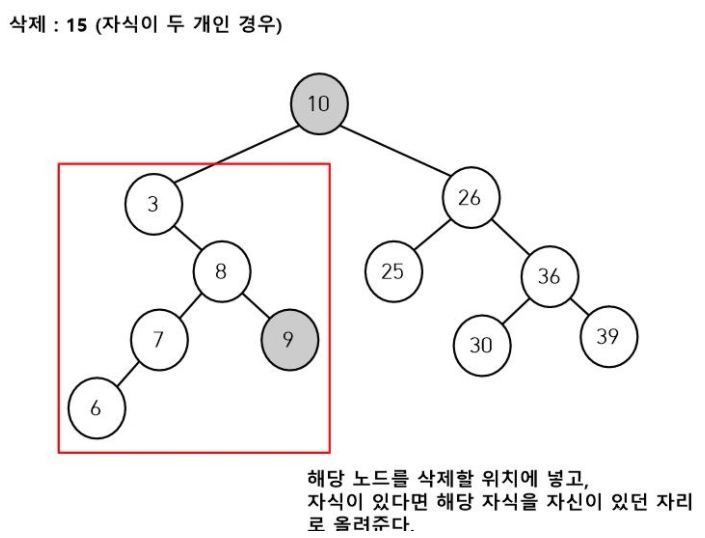
찾은 노드를 삭제 노드 위치로 대체하는 후속 처리를 해줍니다.
그리고 최대값 노드(10이 있던 자리)의 후속 처리또한 필요한데, 이 노드는 자식이 없거나 1개인 경우입니다. (오른쪽 자식이 없는 경우 최대값 노드이므로 해당 노드의 자식은 0개 혹은 1개(왼쪽 자식)이다.)
위에서 설명했던 방법처럼 자식이 없었다면 후속 처리를 할 필요가 없고, 자식이 1개 있다면 자식을 최대값 노드가 있던 위치로 대체해줍니다.
예시에서는 자식이 1개 존재하므로(노드 9) 이를 노드 10이 있던 자리로 대체한 결과입니다.
소스 코드 : https://gist.github.com/fpdjsns/22d923e81d79c426f0e922a8e2a2e28f

참고 : https://ko.wikipedia.org/wiki/%EC%9D%B4%EC%A7%84_%ED%83%90%EC%83%89_%ED%8A%B8%EB%A6%AC
+ 18/10/08
- 루트 노드 삭제되는 경우 수정.
- 삭제 시 삭제 노드 위치를 대체할 노드의 자식 노드가 같이 없어지는 에러 수정.
//141 째 줄
p_max_left->right = NULL; // 대체 노드(왼쪽 서브 트리의 최대값 노드)의 부모노드의 오른쪽 자식 연결 해제
// 수정
p_max_left->right = max_left->left; //부모 노드의 오른쪽 자식에 대체 노드의 왼쪽 노드로 대체한다.
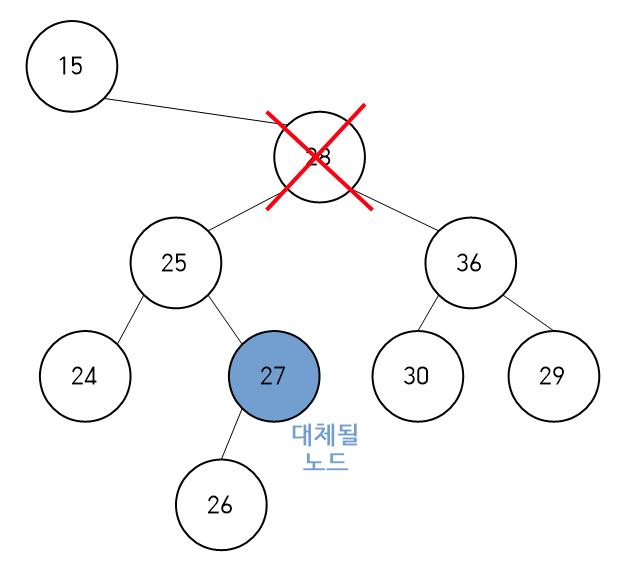

왼쪽이 수정하기 전 코드로 실행 시 삭제 노드 위치에 대체될 노드(27)의 부모 노드(25)의 오른쪽 자식 노드를 NULL로 해준 결과다.
27노드의 왼쪽 자식 노드(26)가 트리의 어느 노드와도 연결되어 있지 않기 때문에 트리에서 제외되어 버린다.
따라서 부모 노드(25)의 오른쪽 자식 노드를 대체되는 노드(27)의 왼쪽 자식 노드(26)에 연결 해주면된다.
대체되는 노드(27)는 애초에 검색 시 오른쪽 자식 노드가 없는 경우를 찾기 때문에 왼쪽 자식만 신경쓰면 된다.


gist 덧글 보고 수정했다. :)
'알고리즘 이론' 카테고리의 다른 글
| [C++/STL] stack을 vector로 변환하기 (0) | 2021.01.21 |
|---|---|
| [DP] 배낭 문제(Knapsack Problem) (0) | 2020.11.28 |
| brian kernighan's algorithm (0) | 2020.07.24 |
| 문자열 해싱(String Hashing) (0) | 2020.06.20 |
| 동전 교환(CC: Coin Change) (5) | 2020.02.23 |

댓글