[Leetcode] 1658. Minimum Operations to Reduce X to Zero
문제 : https://leetcode.com/problems/minimum-operations-to-reduce-x-to-zero/
정수 배열 nums와 정수 x가 입력으로 주어진다.
한 번의 작업으로 배열 nums에서 가장 좌측 혹은 가장 우측에 있는 요소를 제거 하고 x에서 제거한 요소의 값을 뺄 수 있다.
최소 몇 번의 작업으로 x를 정확히 0으로 만들 수 있는지 구하라. 만일 불가능하다면 -1을 반환하라.
부분합과 투포인터로 구할 수 있다.

부분합을 만들어 subsum 배열에 세팅한다.
첫 번째 예제 [1, 1, 4, 2, 3], x=5 로 표를 세팅해보면 [그림1]과 같다.
정답이 되는 제거되는 요소는 가장 뒤 요소 2, 3이다.
이를 반대로 생각하면 제거되지 않는 요소들의 합은 nums 전체 배열 합 11에 x, 5를 뺀 6이 된다.
투 포인터로 제거되지 않는 요소들의 범위를 구하고 이 범위의 합을 subSum 배열로 O(1)만에 구한다.
구한 합이 6과 같다면 해당 범위에 속하지 않은 범위의 요소들의 개수들 중 최소값이 정답이 된다.
만일 범위의 합이 6과 같다면 정답변수와 비교하여 정답변수보다 작다면 정답변수를 갱신한다.
6보다 작다면 범위를 늘려야 하므로 right를 1 증가한다.
6보다 크다면 범위를 줄여야 하므로 left를 1 증가한다.
left는 항상 right 보다 작거나 같아야 한다.
예제 1로 예를 들어보자.

right가 0, left가 0인 경우 범위의 합은 1로 6보다 작다. 따라서 범위 확장을 위해 right를 1 증가시킨다.

right가 1, left가 0인 경우 범위의 합은 2로 6보다 작다. 따라서 right를 1 증가시킨다.

right가 2, left가 0인 경우 범위의 합은 6으로 6과 같다. 따라서 정답일 가능성이 될 수 있기때문에 정답변수를 2(해당 범위에 속하지 않은 요소들의 수)로 갱신한다.
갱신 후 다음 범위 탐색을 위해 right를 1 증가시킨다.

right가 3, left가 0인 경우 범위의 합은 8로 6보다 크다. 범위를 줄이기 위해 left를 1 증가시킨다.
right가 3, left가 1인 경우 범위의 합은 7로 6보다 크다. 범위를 줄이기 위해 left를 1 증가시킨다.
right가 3, left가 2인 경우 범위의 합은 6으로 6과 같다. 따라서 정답일 가능성이 될 수 있기때문에 정답변수를 3(해당 범위에 속하지 않은 요소들의 수)과 비교한다. 정답변수(2)가 더 작기 때문에 갱신하지 않고 다음 범위 탐색을 위해 right를 1 증가시킨다.
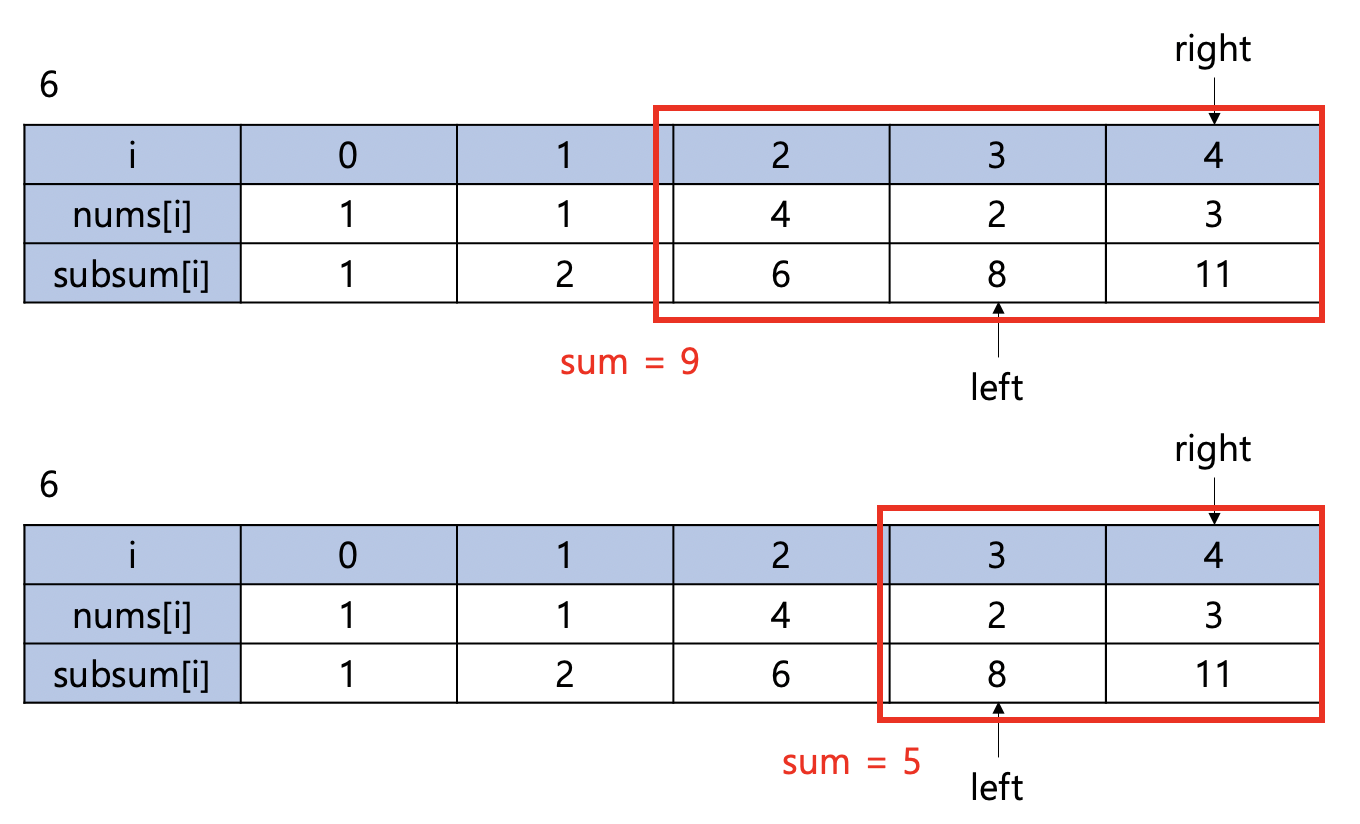
right가 4, left가 2인 경우 범위의 합은 9로 6보다 크다. 범위를 줄이기 위해 left를 1 증가시킨다.
right가 4, left가 3인 경우 범위의 합은 5로 6보다 작다. 범위를 늘리기 위해 right를 1 증가시킨다.
right가 배열 범위를 벗어나기 때문에 탐색을 종료한다.
공간, 시간복잡도는 O(N).
문제 괜찮구먼. 부분합 배열 안만들어도 최신 부분합 값만 가지고 있으면 되므로 공간복잡도 O(1)로 줄일 수 있다.